Допустим, вам необходимо рассчитать количество уникальных строк в файле. Причем, файл большой – миллионы или десятки миллионов строк. Типичный shell’овский однострочник который позволяет решить эту задачу выглядит следующим образом:
sort | uniq | wc -l
И все бы хорошо, но есть одна проблема. Имя ей sort.
Сортировка $O(n \log n)$ по времени и $O(n)$ по памяти, поэтому время её работы очень быстро перерастает все разумные пределы. Как вариант, можно хранить не сами строки, а их контрольные суммы. Это снизит как требования по памяти, так и асимптотическую оценку по времени до $O(n)$. Но хранение контрольных сумм подразумевает наличие коллизий, поэтому вы можете получить не точную оценку, а приблизительную. В случаях когда приблизительной оценки достаточно мы можем разменять точность алгоритма на его скорость и требования к памяти.
Существует один очень простой алгоритм который позволяет вычислять оценку количества уникальных объектов в потоке с довольно высокой точностью за линейное время, используя 0.1 бита на один уникальный объект. Да да, вы не ослышались в одном бите хранится информация о десяти уникальных объектах.
Алгоритм линейного счетчика Link to heading
Ладно, я вас обманул. Невозможно в одном бите хранить информацию о десяти объектах. Но можно хранить тот факт что мы уже встречали хотя бы один из объектов привязанных к этому биту. Именно эта идея лежит в основе алгоритма.
Представьте, что у вас есть битовый вектор из 1000 бит, и вы устанавливаете в нем 1000 случайных бит (некоторые биты будут установлены более одного раза). Если вы теперь посчитаете сколько битов установлено в единицу, то получите число близкое к 630. Если вам интересно почему в итоге получается именно такое число, то об этом я уже писал.
Верно и обратное. Если мы встречаем битовый вектор длины $n$ в котором примерно 63% бит установлено в единицу, это значит что надо этим вектором было произведено примерно $n$ операций установки бита в единицу, при условии что биты выбирались равновероятно.
Таким, довольно нехитрым, способом можно восстановить оценку количества уникальных объектов на основании population count битового вектора (количества бит установленных в единицу). Сделать это можно используя следующую формулу: $ l \log(\frac{l}{N_f}) $, где $l$ — длина вектора, а $N_f$ количество свободных (нулевых) бит (логарифм обязан быть натуральным).
На графике ниже приведена симуляция для вектора длины 10000. В него индексировалось указанное количество объектов, затем получалась доля установленных бит и на её основании восстанавливалась оценка количества добавленных объектов.
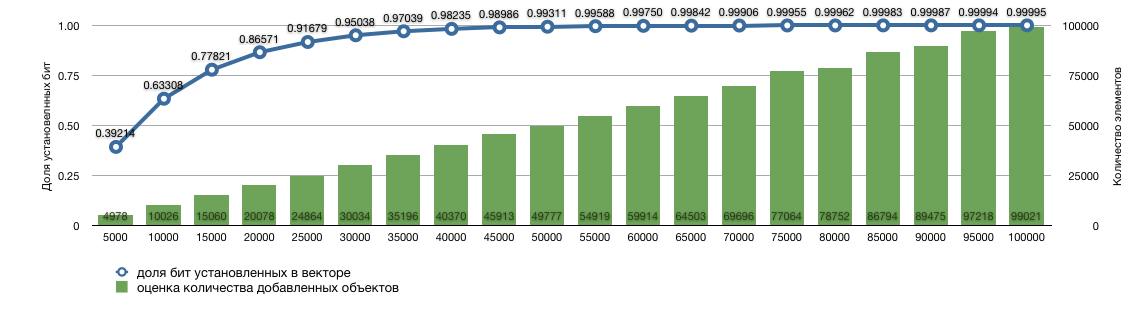
Точность оценки естественным образом связана с отношением количества уникальных объектов к длине битового вектора. Оказывается, что даже если количество добавляемых объектов превышает длину вектора в десять раз, вы по-прежнему можете получать достаточно точные оценки. Погрешность при этом составляет порядка 1%. Это означает, что если в потоке 100 миллионов уникальных объектов, для получения более менее приемлемой оценки достаточно 10 мегабайт памяти.
Реализация Link to heading
Реализация этого алгоритма довольно простая. Самое главное, это хеш-функция с равномерным распределением. Любая криптографическая функция вполне подойдет.
Консольная утилита способная делать быстрый estimate количества уникальных строк в pipe’е иногда очень кстати. Поэтому, я реализовал линейный счетчик на C++. Вы можете использовать этот код в качестве примера. Если же вы пишете на Java, то есть замечательный проект stream-lib в котором помимо линейного счетчика есть масса других вероятностных алгоритмов которые могут оказаться очень полезными при работе с большими массивами данных.
Ссылки по теме Link to heading
- Kyu Y. Whang, Brad T. Vander Zanden, and Howard M. Taylor. A linear-time probabilistic counting algorithm for database applications. ACM Trans. Database Syst., 15(2):208–229, 1990;
- Probabilistic Data Structures for Web Analytics and Data Mining — Ilya Katsov.