В прошлой заметке я в общих чертах описал задачу классификации, а также традиционные подходы используемые для классификации текстовых документов. В этой заметке я более детально расскажу о том как работает самый простой, но вместе с тем один из самых часто используемых при обработке натуральных языков алгоритм классификации – наивный байесовский классификатор.
Заметка разбита на две части: теоретическая, в которой описаны аспекты классификации, и практическая часть построения классификатора. Если вы хотите быстро создать прототип классификатора, то обратитесь к практической части заметки, там на приводится пример классификатора. Также на github доступны исходники примера. Если же вам интересны теоретические принципы работы классификации, то обратитесь к теоретической части заметки.
Теория Link to heading
Осторожно, в этой части заметки много формул.
В основе NBC (Naïve Bayes Classifier) лежит, как вы уже могли догадаться, теорема Байеса.
$$ P(c|d) = \frac{ P(d|c)P(c) }{ P(d) } $$
где,
- $ P(c|d) $ — вероятность что документ $d$ принадлежит классу $c$, именно её нам надо рассчитать;
- $ P(d|c) $ — вероятность встретить документ $d$ среди всех документов класса $c$;
- $ P(c) $ — безусловная вероятность встретить документ класса $c$ в корпусе документов;
- $ P(d) $ — безусловная вероятность документа $d$ в корпусе документов.
Её смысл на обывательском уровне можно выразить следующим образом. Теорема Байеса позволяет переставить местами причину и следствие. Зная с какой вероятностью причина приводит к некоему событию, эта теорема позволяет расчитать вероятность того что именно эта причина привела к наблюдаемому событию.
Цель классификации состоит в том чтобы понять к какому классу принадлежит документ, поэтому нам нужна не сама вероятность, а наиболее вероятный класс. Байесовский классификатор использует оценку апостериорного максимума (Maximum a posteriori estimation) для определения наиболее вероятного класса. Грубо говоря, это класс с максимальной вероятностью.
$$ c_{map}=\operatorname*{argmax}_{c \in C} \frac{ P(d|c)P(c) }{ P(d) }$$
То есть нам надо рассчитать вероятность для всех классов и выбрать тот класс, который обладает максимальной вероятностью. Обратите внимание, знаменатель (вероятность документа) является константой и никак не может повлиять на ранжирование классов, поэтому в нашей задаче мы можем его игнорировать.
Далее делается допущение которое и объясняет почему этот алгоритм называют наивным.
Предположение условной независимости Link to heading
Если я вам скажу “темно как у негра в …”, вы сразу поймете о каком месте чем идет речь, даже если я не закончу фразу. Так происходит потому что в натуральном языке вероятность появления слова сильно зависит от контекста. Байесовский же классификатор представляет документ как набор слов вероятности которых условно не зависят друг от друга. Этот подход иногда еще называется bag of words model. Исходя из этого предположения условная вероятность документа аппроксимируется произведением условных вероятностей всех слов входящих в документ.
$$ P(d|c) \approx P(w_1|c)P(w_2|c)…P(w_n|c) = \prod_{i=1}^n P(w_i|c) $$
Этот подход также называется Unigram Language Model. Языковые модели играют очень важную роль в задачах обработки натуральных языков, но выходят за пределы этой заметки.
Подставив полученное выражение в формулу №1 мы получим:
$$ c_{map}=\operatorname*{arg,max}_{c \in C} \left[ P(c) \prod_{i=1}^n P(w_i|c) \right] $$
Проблема арифметического переполнения Link to heading
При достаточно большой длине документа придется перемножать большое количество очень маленьких чисел. Для того чтобы при этом избежать арифметического переполнения снизу зачастую пользуются свойством логарифма произведения $\log ab = \log a+\log b$. Так как логарифм функция монотонная, ее применение к обоим частям выражения изменит только его численное значение, но не параметры при которых достигается максимум. При этом, логарифм от числа близкого к нулю будет числом отрицательным, но в абсолютном значении существенно большим чем исходное число, что делает логарифмические значения вероятностей более удобными для анализа. Поэтому, мы переписываем нашу формулу с использованием логарифма.
Основание логарифма в данном случае не имеет значения. Вы можете использовать как натуральный, так и любой другой логарифм.
Оценка параметров Байесовской модели Link to heading
Оценка вероятностей $ P(c) $ и $ P(w_i|c) $ осуществляется на обучающей выборке. Вероятность класса мы можем оценить как:
$$ P(c)=\frac{D_c}{D} $$
где, $D_c$ – количество документов принадлежащих классу $c$, а $D$ – общее количество документов в обучающей выборке.
Оценка вероятности слова в классе может делаться несколькими путями. Здесь я приведу multinomial bayes model.
- $W_{ic}$ — количество раз сколько $i$-ое слово встречается в документах класса $c$;
- $V$ — словарь корпуса документов (список всех уникальных слов).
Другими словами, числитель описывает сколько раз слово встречается в документах класса (включая повторы), а знаменатель – это суммарное количество слов во всех документах этого класса.
Проблема неизвестных слов Link to heading
С формулой №3 есть одна небольшая проблема. Если на этапе классификации вам встретится слово которого вы не видели на этапе обучения, то значения $W_{ic}$, а следственно и $P(w_i|c)$ будут равны нулю. Это приведет к тому что документ с этим словом нельзя будет классифицировать, так как он будет иметь нулевую вероятность по всем классам. Избавиться от этой проблемы путем анализа большего количества документов не получится. Вы никогда не сможете составить обучающую выборку содержащую все возможные слова включая неологизмы, опечатки, синонимы и т.д. Типичным решением проблемы неизвестных слов является аддитивное сглаживание (сглаживание Лапласа). Идея заключается в том что мы притворяемся как будто видели каждое слово на один раз больше, то есть прибавляем единицу к частоте каждого слова.
$$ P(w_i|c)=\frac{W_{ic}+1}{ \sum_{i’\in V} \left( W_{i’c} + 1 \right) } = \frac{W_{ic}+1}{ |V| + \sum_{i’\in V} W_{i’c} } $$
Логически данный подход смещает оценку вероятностей в сторону менее вероятных исходов. Таким образом, слова которые мы не видели на этапе обучения модели получают пусть маленькую, но все же не нулевую вероятность. Вот как это выглядит на практике. Допустим на этапе обучения мы видели три имени собственных указанное количество раз.
| Имя | Частота |
|---|---|
| Вася | 3 |
| Петя | 2 |
| Женя | 1 |
И тут на этапе классификации у нас появляется имя Иннокентий, которое мы не видели на этапе обучения. Тогда оригинальная и смещённая по Лапласу оценка вероятностей будет выглядеть следующим образом.
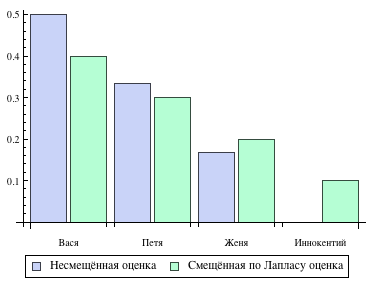
Из графика видно что смещённая оценка никогда не бывает нулевой, что защищает нас от проблемы неизвестных слов.
Собираем все вместе Link to heading
Подставив выбранные нами оценки в формулу №2 мы получаем окончательную формулу по которой происходит байесовская классификация.
Реализация классификатора Link to heading
Для реализации Байесовского классификатора нам необходима обучающая выборка в которой проставлены соответствия между текстовыми документами и их классами. Затем нам необходимо собрать следующую статистику из выборки, которая будет использоваться на этапе классификации:
- относительные частоты классов в корпусе документов. То есть, как часто встречаются документы того или иного класса;
- суммарное количество слов в документах каждого класса;
- относительные частоты слов в пределах каждого класса;
- размер словаря выборки. Количество уникальных слов в выборке.
Совокупность этой информации мы будем называть моделью классификатора. Затем на этапе классификации необходимо для каждого класса рассчитать значение следующего выражения и выбрать класс с максимальным значением.
в этой формуле:
- $D_c$ — количество документов в обучающей выборке принадлежащих классу $c$;
- $D$ — общее количество документов в обучающей выборке;
- $|V|$ — количество уникальных слов во всех документах обучающей выборки;
- $L_{c}$ — суммарное количество слов в документах класса $c$ в обучающей выборке;
- $W_{ic}$ — сколько раз $i$-ое слово встречалось в документах класса $c$ в обучающей выборке;
- $Q$ – множество слов классифицируемого документа (включая повторы).
Информация необходимая для осознания смысла этого выражения приведена выше в разделе Теория.
Пример Link to heading
Допустим, у нас есть три документа для которых известны их классы (HAM означает – не спам):
[SPAM]предоставляю услуги бухгалтера;[SPAM]спешите купить виагру;[HAM]надо купить молоко.
Модель классификатора будет выглядеть следующим образом:
| spam | ham | |
|---|---|---|
| частоты классов | 2 | 1 |
| суммарное количество слов | 6 | 3 |
| spam | ham | |
|---|---|---|
| предоставляю | 1 | 0 |
| услуги | 1 | 0 |
| бухгалтера | 1 | 0 |
| спешите | 1 | 0 |
| купить | 1 | 1 |
| виагру | 1 | 0 |
| надо | 0 | 1 |
| молоко | 0 | 1 |
Теперь классифицируем фразу “надо купить сигареты”. Рассчитаем значение выражения для класса SPAM:
$$ \log\frac{2}{3} + \log\frac{1}{8+6} + \log\frac{2}{8+6} + \log\frac{1}{8+6} \approx -7.629 $$
Теперь сделаем то же самое для класса HAM:
$$ \log\frac{1}{3} + \log\frac{2}{8+3} + \log\frac{2}{8+3} + \log\frac{1}{8+3} \approx -6.906 $$
В данном случае класс HAM выиграл и сообщение не будет помечено как спам.
Формирование вероятностного пространства Link to heading
В простейшем случае вы выбираете класс который получил максимальную оценку. Но если вы например хотите помечать сообщение как спам только если соответствующая вероятность больше 80%, то сравнение логарифмических оценок вам ничего не даст. Оценки которые выдает алгоритм не удовлетворяют двум формальным свойствам которым должны удовлетворять все вероятностные оценки:
- они все должны быть в диапазоне от нуля до единицы;
- их сумма должна быть равна единице.
Для того чтобы решить эту задачу, необходимо из логарифмических оценок сформировать вероятностное пространство. А именно: избавиться от логарифмов и нормировать сумму по единице.
$$ P(c \mid d) = \frac{e^{q_c}}{ \sum_{c’ \in C}e^{q_{c’}} } $$
Здесь $ q_c $ — это логарфмическая оценка алгоритма для класса $ c $, а возведение $ e $ (основание натурального логарфима) в степерь оценки используется для того чтобы избавиться от логарифма ($ a^{\log_a x} = x $). Таким образом, если вы в рассчетах использовали не натуральный логарифм, а десятичный, вам необходимо использовать не $ e $, а 10.
Для вышеприведенного примера вероятность что сообщение спам равно:
$$ \frac{e^{-7.629}}{e^{-7.629} + e^{-6.906}} = 0.327 $$
то есть сообщение является спамом с вероятностью 32.7%.
В комментариях читатели обратили внимание на алгебраическую оптимизацию, которая позволяет избежать арифметического переполнения при делении экспонент друг на друга. Если сократить экспоненту оценки текущего класса в числителе и знаменателе, то в общем виде получим:
$$ P(c \mid d) = \frac{1}{ 1 + \sum_{c^\prime \in C \setminus {c}}e^{q_{c^\prime} - q_c} } $$
Обратите внимание, что сумма в знаменателе выполняется только по классам отличным от того для которого мы считаем вероятность. Но в каждом из слагаемых присутствует логарифмическая оценка оцениваемого класса.
В заключении Link to heading
Show me the code Link to heading
На github доступен пример описанного классификатора реализованный на Scala. Имплементация занимает 50 с лишним строк кода, разобраться с ним у вас не составит труда, просто посмотрите тест ClassifierSpec. Для запуска тестов необходим Maven.
$ mvn test
Вопросы оставшиеся за бортом Link to heading
Сушествует целый ряд вопросов который остался без рассмотрения на текущий момент:
- как тестировать качество алгоритмов классификации;
- какими системными проблемами обладает алгоритм наивной байесовской классификации;
- какие существуют подходы увеличения точности алгоритма.
Учитывая объем данного поста, эти вопросы я смело оставляю для будущих заметок.